Decoding the Mystery – 6/7 as a Decimal

Have you ever found yourself staring at a fraction, wondering what it would look like as a decimal? Perhaps you’re grappling with a math problem, or maybe you’re trying to understand a recipe that calls for a fraction. The world of decimals can seem daunting, but it doesn’t have to be. Today, we’re diving into the intriguing world of fractions and their decimal equivalents, specifically the case of 6/7.

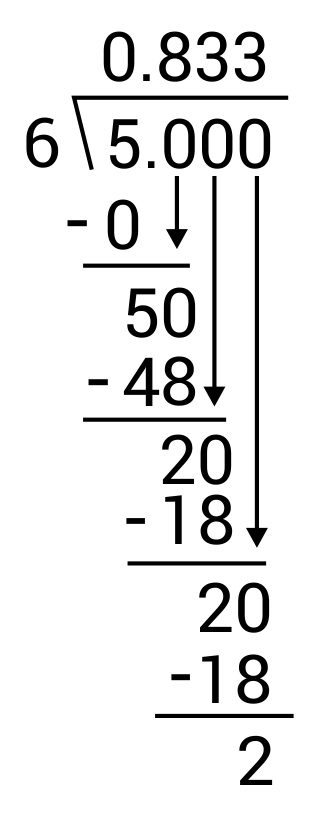
Image: www.1and1is2.com

Fractions, like 6/7, are simply a way of representing parts of a whole. They tell us how many equal pieces there are and how many we’re looking at. Decimals, on the other hand, are a way of representing parts of a whole using place value. They are another way to show the same concept of fractional parts, but with a more convenient system for calculations and applications. In this article, we’ll journey deeper into the conversion of 6/7 into a decimal, understanding its significance and how to use this knowledge for everyday applications.

The Journey from Fraction to Decimal: Unlocking the Secret of 6/7

To transform 6/7 into a decimal, we essentially ask the question, “What is 6 divided by 7?” This division can be performed using a calculator or, if you prefer a more hands-on approach, through long division.

• Long Division: When performing long division, we set up the problem with 7 as the divisor (outside the division symbol) and 6 as the dividend (inside the division symbol).

  • We can add a decimal point and zeros after the 6 to continue the division.
  • You’ll quickly notice that this division doesn’t come out to a whole number. It results in a repeating decimal, which means the same sequence of digits keeps repeating.

• Calculator: If you’re using a calculator, simply type in 6 ÷ 7 and press the equals button. The calculator will give you the decimal equivalent, 0.8571428571.

Therefore, 6/7 as a decimal is 0.8571428571.

Diving Deeper: Understanding Repeating Decimals and Their Significance

Notice that the decimal for 6/7 is a repeating decimal. It’s a pattern that continues forever, and we represent this by placing a bar above the repeating digits.

• Repeating Decimals Explained: Repeating decimals occur when a fraction has a denominator that isn’t a factor of 10 (or any power of 10, like 100, 1000, etc.). In the case of 6/7, the denominator 7 is prime and not a factor of any power of 10. This means we’ll always have a remainder when we divide 6 by 7, leading to the infinite repetition.

Understanding repeating decimals opens doors to a fascinating world of mathematical patterns and challenges.

• Application in Real World: Repeating decimals are often used in situations involving measurements, financial calculations, and engineering. For instance, when dealing with fractions of money or quantities in recipes, converting them into repeating decimals can be helpful for accurate representation.

Unlocking the Practical Side: Using 6/7 as a Decimal in Everyday Life

The knowledge of 6/7 as a decimal can be quite handy in various scenarios:

• Recipes: If a recipe calls for 6/7 cups of flour, you can easily convert it to approximately 0.86 cups. This makes the measurement more accessible if you don’t have a measuring cup that has 1/7th markings.
• Calculations: When you need to calculate a percentage of a specific amount, knowing the decimal equivalent can simplify the process. For example, if you want to find 6/7ths of 140, you can multiply 140 by 0.8571428571, which equals 120.
• Sharing & Division: Let’s say you’re sharing a pizza with 7 friends. You want to divide the pizza fairly, so you divide it into 7 equal slices. If you eat 6 slices, you’ve consumed 6/7ths of the pizza, which is equivalent to 0.8571428571 of the pizza.

Image: byjus.com

Expert Insights: Navigating the World of Fractions & Decimals with Ease

While mastering the conversion of fractions to decimals might seem daunting at first, it’s a valuable skill that can be acquired through practice and understanding. Noted mathematicians and educators emphasize the importance of visual representations, such as diagrams and number lines, for grasping the concept of fractions and their decimal equivalents.

• Practice Makes Perfect: Practice converting various fractions into decimals, gradually working your way up from simpler fractions to more complex ones. As you practice, you’ll develop a sense of familiarity and start recognizing patterns in the conversions.

• Break It Down: When faced with a fraction like 6/7, break down the division process step by step. Visualize the pieces of the whole, and it will become easier to understand the decimal representation.

• Embrace the Power of Technology: Calculators, online converters, and interactive tools can be fantastic resources for exploring fractions and decimals. They provide immediate answers and can offer visual representations to enhance your understanding.

6/7 As A Decimal

https://youtube.com/watch?v=6ZkGMeVhrSA

Concluding Thoughts: A Journey Through the World of Numbers

As our journey into the world of fractions and decimals comes to a close, remember that converting fractions into decimals can be an empowering tool for navigating real-world applications and solving mathematical problems.

Whether you’re encountering fractions in recipes, financial calculations, or everyday scenarios, understanding the decimal equivalent provides you with a versatile representation for easier calculations and a clear understanding of the quantities involved. So, next time you encounter a fraction, take a moment to explore its decimal equivalent and discover the fascinating world of numbers.