Does 5 Divide 1? Exploring Divisibility and Its Implications

Have you ever pondered the question: “Does 5 divide 1?” It may seem like a simple question, and while the answer itself is straightforward, it delves into the fundamental concepts of divisibility, leading to deeper insights into mathematics. Imagine you’re sharing a single pizza with four friends. Can you divide the pizza equally into five slices? The answer, of course, is no. Just like with the pizza, the question “Does 5 divide 1?” challenges our intuitive understanding of division.

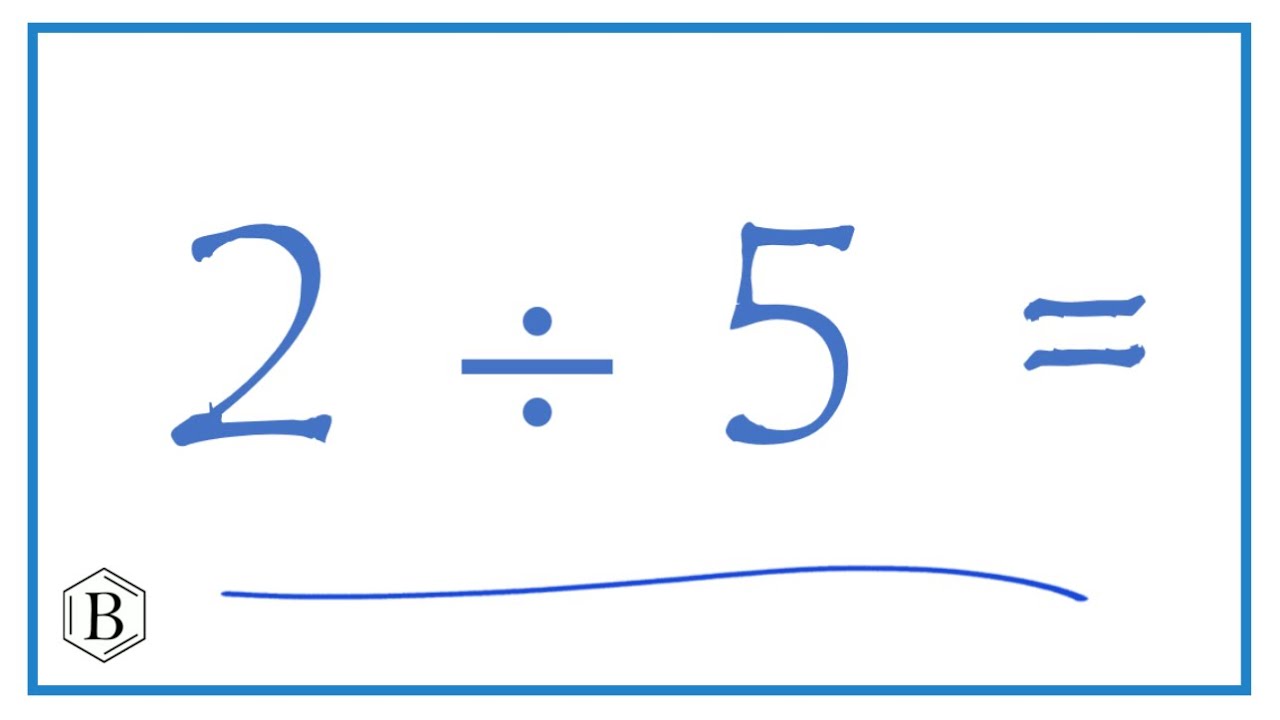
Image: www.youtube.com

This seemingly simple question opens the door to a fascinating exploration of the concept of divisibility. It prompts us to think beyond the familiar world of whole numbers and allows us to explore the broader landscape of mathematical concepts like remainders, factors, and multiples. As we delve deeper into these ideas, we’ll discover how seemingly simple questions like “Does 5 divide 1?” offer a powerful lens through which to understand the intricacies of math.

Divisibility: Understanding the Concept

Divisibility is a core concept in mathematics, referring to the ability of one number to be divided by another number without leaving a remainder. In simpler terms, it’s about whether or not one number can be split into equal parts by another number. When we say “5 divides 1,” we’re asking: Can 1 be divided into 5 equal parts?

The answer, in this case, is no. 1 cannot be divided evenly into 5 parts. Therefore, 5 does not divide 1. When we perform the division 1 ÷ 5, we get a result of 0.2, which is not a whole number. This indicates that we can’t break 1 into 5 equal whole pieces.

Understanding Divisibility Rules

The concept of divisibility introduces us to divisibility rules, a set of quick guidelines that help determine if a number is divisible by another number without actually performing the division. These rules greatly simplify mathematical calculations and offer a shortcut to understanding divisibility relationships.

For instance, one common divisibility rule is that a number is divisible by 2 if its last digit is even. Similarly, a number is divisible by 5 if its last digit is a 0 or a 5. These rules are helpful in everyday scenarios, such as when splitting a bill equally among friends or when determining whether a number of items can be divided evenly into groups.

Exploring the Realm of Factors and Multiples

The question “Does 5 divide 1?” also brings us to the concepts of factors and multiples. Factors are numbers that divide evenly into another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Conversely, multiples are numbers obtained by multiplying a given number by another integer. For instance, the multiples of 5 are 5, 10, 15, 20, and so on.

When we say 5 does not divide 1, we imply that 5 is not a factor of 1. Similarly, 1 is not a multiple of 5. These concepts are interconnected, forming the foundation for understanding mathematical relationships between numbers.

Image: www.nagwa.com

Significance of Divisibility in Mathematics and Beyond

Divisibility plays a crucial role in various mathematical fields, including number theory, algebra, and cryptography. Determining divisibility helps us identify prime numbers, understand modular arithmetic, and solve mathematical equations. Furthermore, divisibility concepts extend beyond the purely mathematical realm.

In everyday life, we encounter divisibility in scenarios such as splitting a bill equally among friends, dividing items for distribution, or organizing objects into groups. Understanding divisibility allows us to make informed decisions about how to distribute resources or allocate tasks efficiently.

Divisibility in the Digital Age: Applications in Computer Science

The impact of divisibility extends to the digital age, where it plays a crucial role in computer science. Divisibility concepts are fundamental to algorithms used in data encryption, error detection and correction codes, and hash functions. These applications ensure secure online transactions, accurate data transmission, and efficient data storage and retrieval.

Furthermore, divisibility principles are embedded in the design of computer components. Processor architectures and memory allocation often rely on divisibility to optimize performance and utilize resources effectively. From the encryption algorithms that safeguard our online communications to the underlying structure of our digital devices, divisibility remains a crucial element in the modern digital world.

Tips and Expert Advice for Understanding Divisibility

Here are some tips and expert advice to improve your understanding of divisibility:

– Master Divisibility Rules: Familiarize yourself with the divisibility rules for different numbers. Practice them regularly to enhance your ability to quickly determine whether one number divides another without performing lengthy calculations.
– Explore Prime Numbers: Prime numbers, which have only two factors (1 and themselves), are foundational to divisibility. Understanding prime numbers provides a deeper insight into the nature of divisibility and its various applications.
– Engage in Mathematical Puzzles: Challenge yourself with mathematical puzzles and problems that involve divisibility. This hands-on approach will solidify your understanding and expand your problem-solving skills.

FAQ: Frequently Asked Questions About Divisibility

Q: What is the remainder when 1 is divided by 5?
A: The remainder when 1 is divided by 5 is 1. This is because 1 cannot be divided evenly into 5 parts, leaving a remainder of 1.

Q: How can I determine if a number is divisible by 3?
A: A number is divisible by 3 if the sum of its digits is divisible by 3. For example, 123 is divisible by 3 because 1 + 2 + 3 = 6, which is divisible by 3.

Q: What is the significance of zero in divisibility?
A: Zero is divisible by every non-zero number because any number multiplied by zero equals zero. Therefore, any non-zero number divides zero.

5 Divides 1

Conclusion

The question “Does 5 divide 1?” may seem deceptively simple, but it leads to a fascinating exploration of divisibility, factors, multiples, and their implications in mathematics and other fields. From everyday scenarios to the intricate world of computer science, divisibility plays a pivotal role in understanding numerical relationships and maximizing efficiency.

Are you interested in learning more about divisibility? Dive deeper into the subject and explore the intriguing world of numbers.