Z Angle – A Quirky Geometric Shape and Its Applications

Have you ever noticed how easily a zig-zag pattern catches your eye? The sharp turns, the alternating direction, it’s almost as if the pattern itself is trying to tell you something. This pattern, with its repeated “Z” shape, is more than just a visually appealing design element. It’s a foundational concept in geometry: the Z angle.

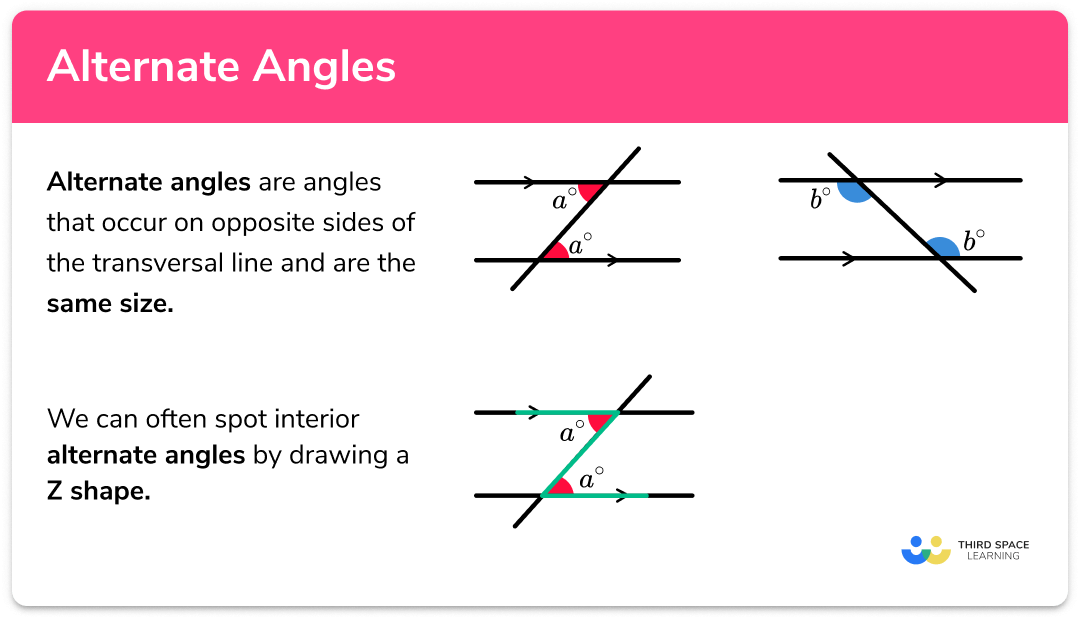
Image: www.buickcafe.com

A Z angle, or a “zig-zag” angle, is a specific arrangement of two lines intersected by a third line, creating two pairs of equal angles. This seemingly simple arrangement holds a powerful punch in the world of geometry. Imagine creating intricate designs, analyzing the structural integrity of bridges, or navigating the vast expanse of space – Z angles play a crucial role in all these activities. This article dives into the fascinating world of the Z angle, exploring its fundamental principles, real-world applications, and its role in shaping our understanding of the world.

Understanding Z Angles: The Foundation

To decode the magic of Z angles, let’s unpack the basics. Visualize two parallel lines intersected by a third line, known as a “transversal”. This intersection forms eight distinct angles, and the Z angle signifies a special relationship between these angles. Specifically, it refers to two non-adjacent angles on opposite sides of the transversal. These angles, known as **alternate interior angles**, are always equal in measure.

Example Time:

Imagine drawing two parallel lines on a piece of paper. Now, draw a diagonal line across both parallel lines. You’ll have eight angles formed. Focus on any two non-adjacent angles that fall on opposite sides of the diagonal line, inside the parallel lines. These are your Z angles. The magic is that these two angles will always be identical in their degree measurement. This fundamental principle of the Z angle, also known as the **alternate interior angle theorem**, is the key to understanding many complex geometric concepts and applications.

Beyond the Basics: Z Angles in Action

The Z angle is not just a theoretical concept confined to textbooks. It is a powerful tool used in diverse fields, from engineering to architecture to navigation.

Image:

1. Construction and Architecture:

Imagine you’re building a bridge. The bridge needs to distribute weight evenly and maintain its structural integrity. Here, Z angles enter the scene. The truss structure, a common feature in bridges and other large structures, utilizes Z angles to transfer forces efficiently. The diagonal members of a truss form Z angles, allowing for strength and stability. Understanding the properties of Z angles helps engineers design structures that can withstand immense forces, ensuring safety and reliability.

2. Navigation and Surveying:

For sailors navigating vast oceans and surveyors mapping vast terrains, Z angles are vital. Determining the position of objects relies on angles, and Z angles help in calculating distances and angles precisely. Navigators use Z angles to calculate bearings, while surveyors use them to measure distances and map out land. From charting the course of a ship to designing intricate maps, Z angles are instrumental in understanding and representing our world.

3. Computer Graphics:

The world of computer graphics is filled with Z angles. Perspective drawing, a technique that creates the illusion of depth on a flat surface, relies heavily on the principles of Z angles. By manipulating angles and creating Z-shaped arrangements, artists can create realistic 3D representations of objects in a 2D space. Z angles also play a critical role in computer-aided design (CAD) software, allowing engineers to model and create objects in virtual spaces with precision.

Z Angles: Unveiling the Secrets of Geometry

The Z angle is more than just a geometric concept; it’s a window into a deeper understanding of the world around us. It helps us comprehend the fundamental principles of geometry and apply those principles in countless practical applications. Whether you’re designing a skyscraper, charting a course, or simply admiring a visually striking pattern, the Z angle is an integral part of the rich tapestry of geometry that shapes our everyday lives.

Z Angle

Explore Further:

If you’re captivated by the wonders of Z angles and the world of geometry, there is a universe of information waiting to be explored. Delve into books and websites dedicated to geometry, explore interactive simulations showcasing geometric principles, and maybe even try your hand at creating your own Z-angle-driven art or designs.