Unveiling the Harmony – Exploring the LCM of 4 and 10

Have you ever found yourself organizing a group of friends for a movie night, with everyone wanting snacks but only certain quantities available? You need to find the smallest amount of snacks that will be divisible by the number of friends in each group. This is where the concept of the least common multiple (LCM) comes into play, helping you avoid any leftover snacks and ensure everyone gets their fair share. The LCM is a fundamental concept in mathematics that plays a crucial role in various areas, from everyday scenarios like planning events to complex mathematical operations.

Image: www.youtube.com

In this article, we delve into the intriguing world of the LCM, specifically focusing on the LCM of 4 and 10. We’ll explore its definition, calculation methods, and real-world applications, taking you on an engaging journey through the heart of this essential mathematical concept. Whether you’re a student grappling with basic arithmetic or an enthusiast seeking to expand your mathematical knowledge, this exploration will equip you with a deeper understanding of the LCM and its significance in our daily lives.

Understanding the Least Common Multiple (LCM)

The least common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by all the given numbers. Imagine it as finding the smallest common ground where all the numbers can align perfectly. It’s like finding the smallest number that acts as a common denominator for fractions, ensuring smooth calculations. The LCM is a fundamental concept in mathematics with a wide range of applications.

Visualizing the LCM

To visualize the LCM, let’s think about a scenario where we have two groups of people: one group with 4 people and another with 10 people. We want to arrange them in equal rows, maximizing the number of people in each row. The LCM will tell us the maximum number of people we can have in each row while still having equal rows for both groups.

Finding the LCM: Prime Factorization

One of the most common ways to find the LCM is through prime factorization. This method involves breaking down each number into its prime factors, then taking the highest power of each prime factor that appears in either number. The product of these highest powers gives us the LCM.

• Prime factorize 4: 2 × 2 = 2²
• Prime factorize 10: 2 × 5
• Identify the highest powers of each prime factor: 2² × 5
• Multiply the highest powers: 2² × 5 = 4 × 5 = 20

Therefore, the LCM of 4 and 10 is 20.

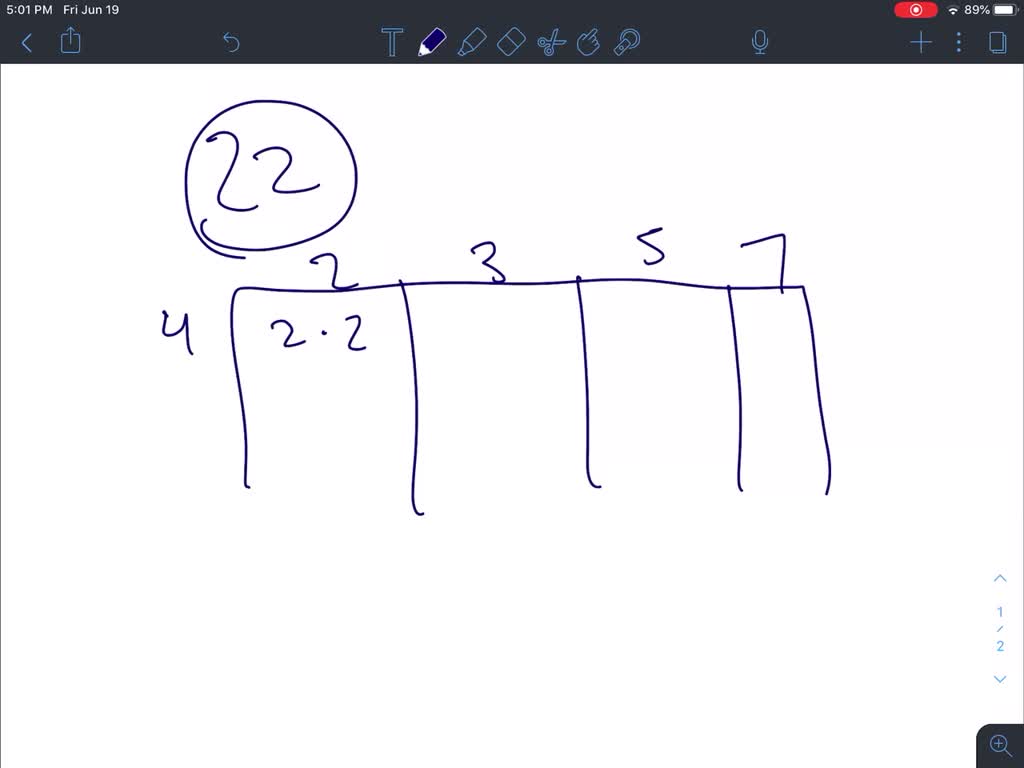
Image: www.numerade.com

Finding the LCM: Listing Multiples

Another method, albeit less efficient for larger numbers, involves listing the multiples of each number until a common multiple is found.

• Multiples of 4: 4, 8, 12, 16, 20, 24, 28…
• Multiples of 10: 10, 20, 30, 40…

The smallest common multiple is 20, verifying our previous result.

Real-world Applications of the LCM

The LCM has numerous practical applications across various fields. Its ability to find the smallest common ground makes it relevant in scenarios like:

Event Planning

Suppose you’re organizing a party with two groups of guests: one group of 4 people and another group of 10 people. You want to divide them into equal teams for a game. To ensure everyone is in a team, the LCM (20) will tell you the maximum number of people you can have in each team, guaranteeing everyone participates.

Fractions and Arithmetic

The LCM plays a crucial role in working with fractions. When adding or subtracting fractions, you need to find a common denominator, which is precisely the LCM of the denominators. This ensures that the fractions are expressed in the same units, allowing for accurate calculations.

Clocks and Time

Imagine two clocks, one ticking every 4 hours and the other ticking every 10 hours. The LCM, 20, will tell you when both clocks will tick simultaneously. This concept is helpful in understanding the synchronized behavior of periodic events, such as the alignment of planetary bodies.

Music and Rhythm

The LCM is essential in music, particularly in understanding musical rhythms. The LCM of two different rhythmic patterns helps determine when the patterns will align, creating a harmonious musical experience. A common example is in a piece where a melody repeats every 4 beats while a bass line repeats every 10 beats. The LCM, 20, tells us that both patterns will align after 20 beats, creating a rhythmically cohesive sound.

Computer Programming

In computer programming, the LCM is used in algorithms that involve scheduling tasks or allocating resources. Optimizing the allocation of resources can be done by finding the LCM of the different time intervals for tasks, ensuring that resources are used efficiently without conflicts.

Exploring the Significance of the LCM

Understanding the LCM extends beyond simply finding a common multiple. Its significance lies in its ability to unify different units or measurements, creating a shared ground for comparison and calculation. It’s the mathematical language that allows us to harmonize diverse elements, finding common ground in seemingly disparate situations.

The LCM in Everyday Life

Even in everyday life, the LCM subtly guides our actions. Consider shopping for groceries. You might buy a pack of 4 apples and another pack of 10 oranges. To split them equally among friends, you’d aim for a quantity divisible by both 4 and 10, unknowingly applying the LCM principle.

Expanding Your Mathematical Horizons

The LCM is a stepping stone to understanding more intricate mathematical concepts. It provides a foundation for tackling advanced topics such as modular arithmetic, which has applications in cryptography and computer science. As we navigate through more complex mathematical landscapes, understanding the LCM empowers us to make sense of seemingly abstract ideas, forging connections between diverse branches of mathematics.

Lcm Of 4 And 10

Conclusion

The LCM, often hidden in plain sight, plays a pivotal role in harmonizing different elements, from organizing events to performing arithmetic. Whether you’re a student, a musician, or simply curious about the world around you, grasping the concept of the LCM empowers you to navigate the complexities of everyday life and delve deeper into the elegance of mathematics. As you embark on your journey of mathematical exploration, remember that the LCM is a fundamental building block, waiting to be discovered and appreciated in all its mathematical beauty.