Turning 0.5 into a Fraction – A Simple Guide

Ever wondered how to represent a number like 0.5 as a fraction? It might seem daunting at first, but the process is surprisingly straightforward. Understanding this concept can be incredibly useful in various areas, from everyday math problems to more advanced applications in fields like science and engineering. So, let’s dive into the world of decimals and fractions, and uncover the magic of transforming 0.5 into its fractional equivalent.

Image: whatihavelearnedteaching.com

Imagine you’re baking a cake and the recipe calls for 0.5 cups of flour. While you might have a measuring cup with markings for fractions like 1/2, it’s helpful to understand how to express 0.5 as a fraction to adapt recipes or understand quantities in other contexts. This practical scenario underscores the significance of understanding how to convert decimals to fractions, a skill that can simplify calculations and improve your grasp of numerical concepts.

Understanding Decimals and Fractions

Before we embark on the journey of converting 0.5 into a fraction, let’s establish a clear understanding of what decimals and fractions represent.

Decimals:

Decimals, like 0.5, represent parts of a whole number. The decimal point separates the whole number part from the fractional part. In 0.5, the “0” indicates that there are no whole numbers, and the “5” represents five tenths (5/10) of a whole.

Fractions:

Fractions, on the other hand, express parts of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts of the whole are being considered, while the denominator represents the total number of parts in the whole. For example, the fraction 1/2 indicates one out of two equal parts.

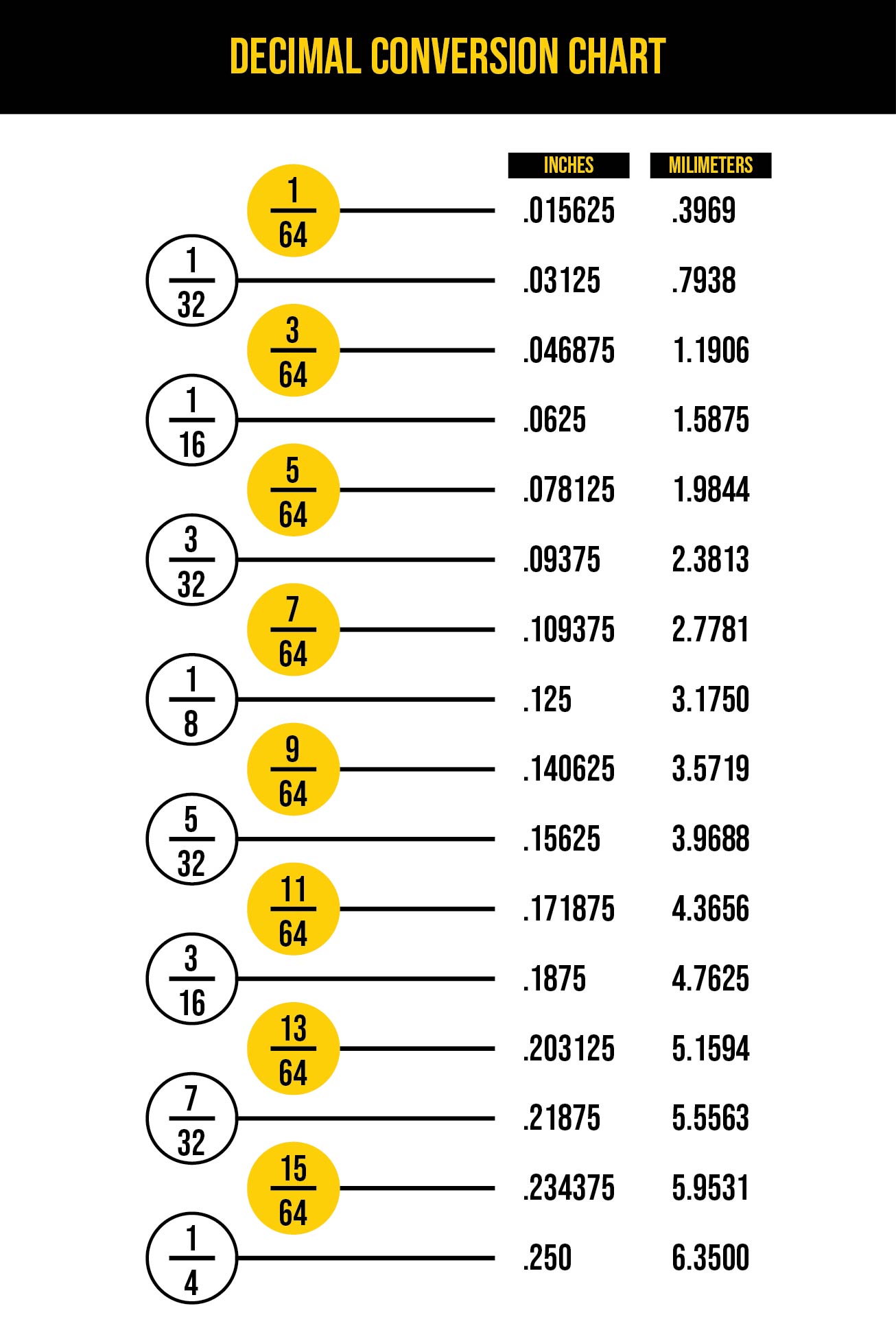
Image: lessonberginsampling.z21.web.core.windows.net

Converting Decimal to Fraction: The Steps

Now, let’s delve into the practical process of turning 0.5 into a fraction. Follow these simple steps:

1. Identify the Decimal Place

Start by recognizing the decimal place value. In 0.5, the digit “5” is in the tenths place, meaning it represents five-tenths of a whole.

2. Express as a Fraction

Write the decimal as a fraction with the decimal value as the numerator and the corresponding place value as the denominator. In this case, 0.5 becomes 5/10.

3. Simplify

The last step is to simplify the fraction, if possible, by finding the greatest common factor (GCF) of the numerator and denominator. In this instance, the GCF of 5 and 10 is 5. Divide both the numerator and denominator by 5, resulting in 1/2.

Illustrative Examples

To solidify your understanding, let’s explore a few more examples of converting decimals to fractions:

• 0.25: The decimal “25” is in the hundredths place, so we express it as 25/100. Simplifying by dividing both numerator and denominator by 25, we get the fraction 1/4.

• 0.75: With “75” in the hundredths place, we have the fraction 75/100. Simplifying by dividing both numerator and denominator by 25, we arrive at the fraction 3/4.

• 0.6: The decimal “6” is in the tenths place, so we write it as 6/10. Simplifying by dividing both numerator and denominator by 2, we get the fraction 3/5.

Real-World Applications

Converting decimals to fractions is a fundamental math skill that finds applications in various real-world scenarios:

• Cooking and Baking: Recipes often use fractions to indicate ingredient quantities. Understanding decimal to fraction conversion allows you to adapt recipes easily.

• Construction and Engineering: Engineers and architects use fractions and decimals to calculate dimensions and measurements with precision.

• Finance and Budgeting: Financial transactions often involve decimals, and converting them to fractions helps analyze and understand financial data better.

• Science and Research: Scientific calculations often rely on decimals and fractions for accurate measurements and data representation.

05 Into Fraction

Conclusion

Converting decimals like 0.5 to fractions is a valuable skill for navigating various mathematical and practical situations. By understanding the process of identifying the decimal place value and expressing it as a fraction, you can confidently transform decimals into their fractional equivalents. This knowledge proves useful in various fields, solidifying your understanding of numbers and enhancing your problem-solving abilities. So, whether you’re baking a cake or tackling complex scientific calculations, the ability to convert decimals to fractions will serve you well.