3 5 8 as a Decimal – A Closer Look

Have you ever wondered what happens when you try to express the seemingly straightforward number sequence “3 5 8” as a decimal? It might seem like a simple conversion, but there’s a bit more to it than meets the eye. This seemingly simple question actually opens a door to some fascinating discussions about the nature of numbers, their representations, and the importance of precision in mathematical communication.

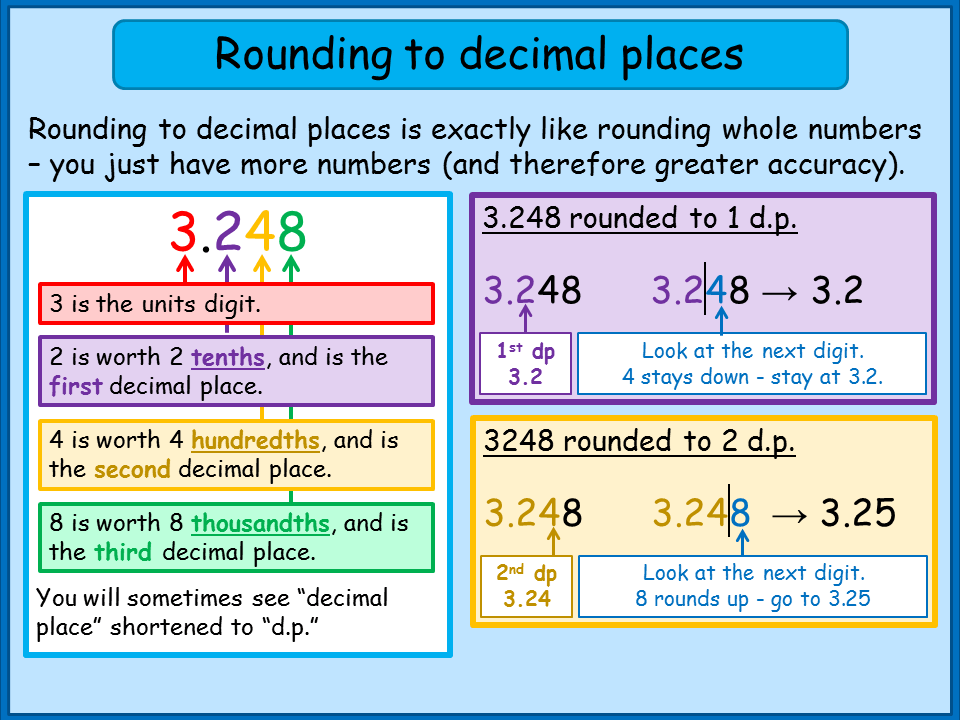
Image: studyzonequaaludes.z13.web.core.windows.net

In the realm of mathematics, representing numbers in different forms is a fundamental concept. Decimals, with their ability to express fractions and values beyond whole numbers, are a powerful tool. But, just like any tool, they come with rules and nuances that we need to understand. When it comes to “3 5 8” as a decimal, the key lies in recognizing the missing information: what does this sequence actually represent? Is it a whole number, a fraction, or something else entirely?

Interpreting the Mystery: What Does “3 5 8” Represent?

The first hurdle in converting “3 5 8” to a decimal is figuring out what kind of number it is. Without context, “3 5 8” could represent several different things:

1. A Whole Number

If “3 5 8” is simply a whole number, then the conversion is straightforward. It’s already in decimal form: **358**.

2. Three Separate Numbers

It’s also possible that “3 5 8” represents three distinct whole numbers, “3”, “5”, and “8”. In this case, converting them to decimals would simply be **3.0**, **5.0**, and **8.0**.

Image: yasmeenscott.blogspot.com

3. A Fraction

Perhaps “3 5 8” is intended to represent a fraction, but without additional clues, we can’t be sure. There are a few possibilities here:

• **3/58:** This would mean “3 divided by 58.”
• **35/8:** This would mean “35 divided by 8.”
• **3/5/8:** This could be interpreted as a complex fraction, “3 divided by 5, then divided by 8.”

Each of these fractions would yield different decimal values after conversion.

The Importance of Context and Clarity

This simple example highlights the importance of clarity in mathematical communication. If we don’t know the intended meaning of “3 5 8”, we can’t definitively convert it to a decimal. It’s crucial to understand the context and what kind of number is being represented.

Exploring the Different Decimal Conversions

Now, let’s assume “3 5 8” is meant to represent a fraction. We’ll explore the possibilities we listed earlier and convert them to decimal form:

1. 3/58

To convert 3/58 into a decimal, we perform the division: 3 divided by 58. The result is approximately **0.0517**.

2. 35/8

Converting 35/8 into a decimal involves dividing 35 by 8. This results in **4.375**.

3. 3/5/8

Converting the complex fraction 3/5/8 requires performing the divisions in order:

• First, we divide 3 by 5, resulting in 0.6.
• Then, we divide 0.6 by 8, resulting in **0.075**.

The Power of Decimals

Let’s take a moment to appreciate the power of decimals. They allow us to express values that fall between whole numbers. Fractions are essentially another way to represent parts of a whole, and decimals offer a convenient way to express these parts in a standardized form.

In the real world, decimals are used extensively in various fields. From financial transactions to scientific measurements, the ability to represent precise values is crucial.

For example, in a stock market report, a stock might be quoted at $15.25. This decimal representation immediately conveys the price in dollars and cents. Imagine trying to express this same information using fractions! Decimals offer a much simpler and more efficient way to represent such values.

Beyond Numbers: Decimals in Everyday Life

The concept of decimals extends beyond just representing numbers. They play a significant role in our daily lives in unexpected ways. Have you ever noticed that a digital clock displays the time using decimals? For instance, 10:35 AM could be written as 10:35.00. This use of decimals provides a way to denote precise time with even seconds.

In the realm of technology, decimals are crucial for computer programming, data analysis, and even the functioning of our digital devices. These seemingly simple numbers form the foundation for countless processes upon which our modern world relies.

3 5 8 As A Decimal

https://youtube.com/watch?v=ec5D8xlSx3s

Conclusion

The question “3 5 8 as a decimal” may seem straightforward, but it opens up a fascinating exploration of number representations, context, and the importance of clarity in mathematical communication. We saw that understanding the context of a number sequence is essential for accurate conversion, and explored the different decimal values that could arise from various interpretations. By understanding decimals and their diverse applications, we gain a deeper appreciation for their role in our world, from financial transactions to technological advancements.

So, the next time you encounter a number sequence like “3 5 8”, take a moment to consider the potential meanings behind it. Understanding the context can unlock a world of possibilities and reveal the hidden power of seemingly ordinary numbers.