Have you ever found yourself staring at a pizza, wondering how many slices it would take to make up a certain portion? Or perhaps you’re trying to divide a recipe in half, and you need to figure out what fractions to use. These everyday scenarios highlight the importance of understanding fractions, and one common question that arises is, “How many 1/4s are in 3/4?”
Image: www.gauthmath.com
This question, seemingly simple yet fundamental, opens a door to a fascinating world of fractions. It’s a stepping stone to understanding how to compare, add, subtract, and even multiply fractions, skills that are essential for navigating various aspects of our lives. In this article, we’ll delve into the world of fractions, uncovering the answer to this question and exploring why it matters for everyday life.
Understanding the Basics of Fractions
Before diving into the specific question, let’s first solidify our understanding of what fractions are. A fraction represents a part of a whole. It is composed of two numbers: the numerator, which sits above the line and indicates the number of parts we have, and the denominator, which is below the line and shows the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator 3 tells us we have 3 parts, and the denominator 4 tells us the whole is divided into 4 equal parts. So, 3/4 represents 3 out of the 4 total parts.
Visualizing Fractions: A Pie Chart Approach
Often, the most effective way to understand fractions is through visualization. Imagine a circular pie cut into 4 equal slices. Each slice represents 1/4 of the whole pie. If we take 3 of these slices, we have 3/4 of the pie, as illustrated below:
Image: A pie chart divided into 4 slices. 3 slices are shaded, representing 3/4 of the pie.
Finding the Answer: How Many 1/4s in 3/4?
Now that we have a clear grasp of fractions, let’s tackle the original question. How many 1/4s are in 3/4?
Referring back to our pie chart, we can see that 3/4 of the pie is made up of 3 of the 1/4 slices. Therefore, there are 3 1/4s in 3/4.
Another way to think about it is that 3/4 is the same as 3 times 1/4. So, if we multiply 1/4 by 3, we get 3/4, confirming our answer.
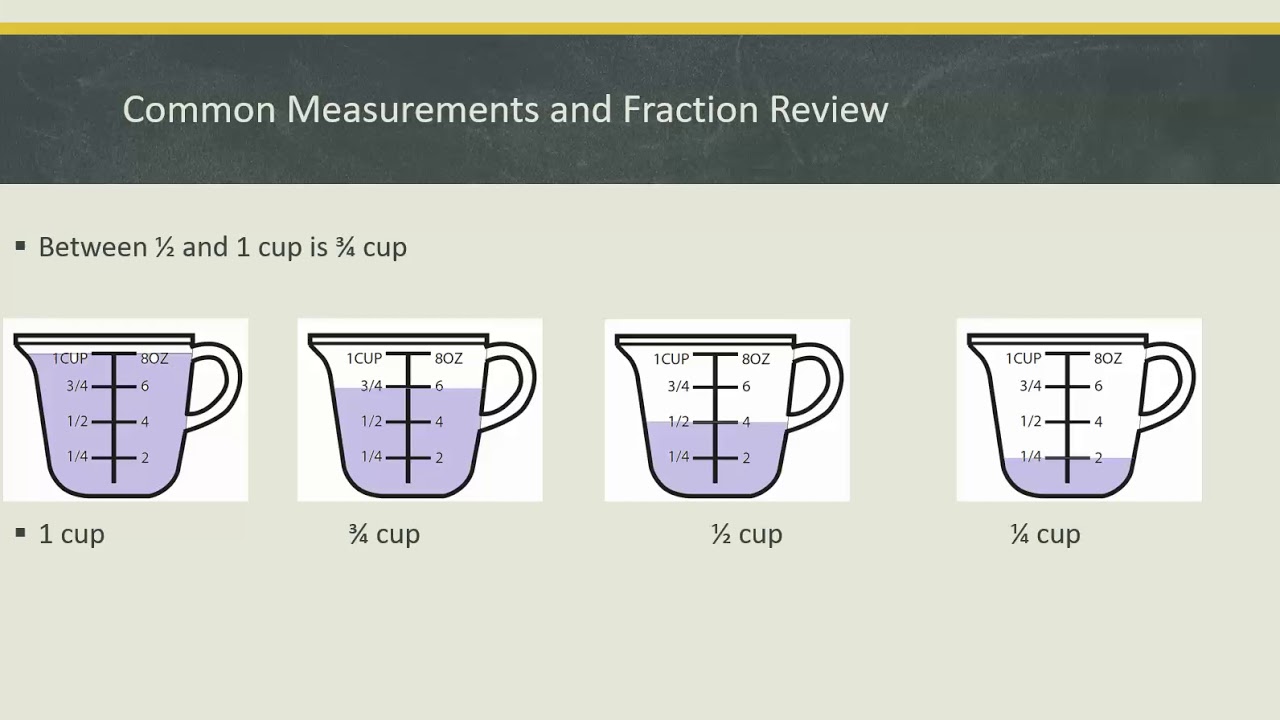
Image: bmxracingthailand.com
Applications of Fractions in Everyday Life
Understanding fractions is essential for many real-world applications.
Cooking and Baking
When following a recipe, you often need to divide ingredients or adjust quantities. For instance, a recipe might call for 1/2 cup of flour but you only have 1/4 cup. Knowing that 2 x 1/4 = 1/2 can help you adapt the recipe accordingly.
Measuring and Construction
Tradespeople like carpenters and plumbers work with fractions constantly. Measuring lengths, cutting materials, and calculating angles often involve fractions, whether it’s inches, feet, or even degrees of a circle.
Money and Finance
Fractions are crucial in dealing with money. Understanding interest rates, discounts, and percentages often requires working with fractions.
Time Management
We use fractions to conceptualize time. A quarter hour is 1/4 of an hour, and a half hour is 1/2. We can use fractions to plan our schedules, break down tasks, and track progress.
Beyond the Basics: Exploring Fraction Operations
Understanding how many 1/4s are in 3/4 is a great starting point. Let’s explore some more advanced concepts and operations with fractions:
Adding and Subtracting Fractions
To add or subtract fractions that have the same denominator, we simply work with the numerators. For example, 2/5 + 1/5 = 3/5. However, for fractions with different denominators, we need to find a common denominator before adding or subtracting. This involves finding the least common multiple of the two denominators.
Multiplying Fractions
Multiplying fractions is relatively straightforward. We simply multiply the numerators and the denominators. For example, 2/3 x 1/2 = (2 x 1) / (3 x 2) = 2/6.
Dividing Fractions
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by flipping the numerator and denominator. For instance, the reciprocal of 2/3 is 3/2. Therefore, 4/5 ÷ 2/3 = 4/5 x 3/2 = 12/10.
How Many 1/4 In 3/4
Conclusion: The Power of Fractions
Understanding how many 1/4s are in 3/4 is a simple yet powerful concept that unlocks a world of possibilities. It equips us with the tools to tackle everyday situations, from cooking and baking to construction and finance. Learning about fractions is a vital step towards numeracy, opening doors to a wider understanding of the world around us. So, next time you encounter a fraction, remember that it’s not just a number on a page but a key that can unlock a world of opportunities.

:max_bytes(150000):strip_icc()/OrangeGloEverydayHardwoodFloorCleaner22oz-5a95a4dd04d1cf0037cbd59c.jpeg?w=740&resize=740,414&ssl=1)




